Ein Operationscode (opcode) der JVM wird repräsentiert durch ein vorzeichenloses
Byte. Jedem dieser Bytes ist eine Mnemonik zugerordnet. Der vollständige Befehlssatz
der Java Virtual Machine wird innerhalb der
Java Virtual Machine Specification
 detailliert beschrieben.
detailliert beschrieben.
Kennzeichnung und Wertigkeit von JVM-Befehlen
Ein JVM-Befehl besteht aus einem Operationscode, der angibt, welche Operation
ausgeführt werden soll und aus möglicherweise darauffolgenden Operanden, die für
die Operation benötigt werden. Mögliche Operanden-Bytes folgen direkt im Anschluss
an das Byte, das den Opcode repräsentiert. Bei datenabhängigen Operationen
werden die Operationsbezeichnungen (Mnemoniks) mit Buchstaben gekennzeichnet. So
bedeuted die Abkürzung iadd, dass zwei Werte vom Typ int
addiert werden, wohingegen fadd eine Addition zweier
float-Werte vornimmt. Die folgende Übersicht zeigt die Zuordnung der
verwendeten Buchstaben zum Datentyp:
| Buchstabe | Typ |
i |
int |
l |
long |
s |
short |
b |
byte |
c |
char |
f |
float |
d |
double |
a |
reference |
Als Beispiele für JVM-Befehle mit unteschiedlicher Anzahl von Bytes (Operanden-Bytes) sollen einige Befehle genannt werden. Die folgenden Anweisungen besitzen der Reihe nach kein Operanden-Byte, ein Operanden-Byte und zwei Operanden-Bytes:
| Assembler | Bytecode |
iadd |
60 |
bipush 9 |
10 09 |
sipush 303 |
11 01 2f |
Der Befehl iadd ist einwertig, d.h. er wird im Bytecode durch
ein einzelnes Byte repräsentiert. Der genannte Additionsbefehl setzt voraus, dass
sich die zu addierenden Zahlenwerte auf dem Operandenstack befinden. Erscheint also
innerhalb einer Klassendatei (Methodenbereich) die Zahl 60 (hex.) dann werden
automatisch zwei Zahlen, die im Integer-Format vorliegen müssen, vom Stapel geholt,
addiert und das Ergebnis wird anschließend wieder auf den Operandenstack gelegt.
Da der Befehlssatz der JVM viele einwertige Befehle besitzt kann ein Programm
relativ kompakt in einer Klassendatei repräsentiert werden.
Beschreibung des Operandenstapels
Bei der Beschreibung von Befehlen, die mit Hilfe des Operandenstacks
abgearbeitet werden, ist es hilfreich eine Oprandenstack-Beschreibung zu nennen.
Für den Additonsbefehl iadd
würde eine derartige Beschreibung des Stapels wie folgt lauten:
Operandenstapel bei iadd: ..., value1,
value2 --> ..., result
Der Wert value2 liegt vor der Addition (linke Seite vom Pfeil) an oberster
Stelle des Stapels. Nach der Addition (rechte Seite vom Pfeil) befindet sich
value1 und value2 nicht mehr auf dem Operandenstack, sondern nur das Endergebnis
result. Die drei aufeinanderfolgenden Punkte in der Darstellung stehen für Werte,
die sich bereits auf dem Stapel befinden aber für die betrachtete Operation nicht
interessant sind. Die folgende Übersicht zeigt ein Additionsbeispiel, wobei
der Programmausschnitt innerhalb einer statischen main-Methode steht.
Die JVM-Befehle, die diesen Quelltext realisieren, sind in der zweiten Spalte
aufgeführt. Die einzelnen Anweisungen haben Auswirkungen auf den Frame der Methode.
Die beiden Elemente Operandenstapel und Array der lokalen Variablen des Frames
sind in den weiteren Spalten notiert, wobei die Änderungen auf diese Elemente
sichtbar werden. Im genannten Array steht bei Index 0 eine Referenz auf das bekannte
String-Array, das einer main-Methode als einziges
Argument übergeben wird. Das dargestellte Array der lokalen Variablen besteht
aus vier Elementen, wobei bei Index 1 die Variable value1, bei Index 2 die Variable
value2 und bei Index 3 das Ergebnis result der Berechnung eingetragen ist.
| Programmausschnitt | JVM-Befehle | Operandenstapel | lokale Variablen |
int value1 = 3; |
iconst_3 |
... --> ..., 3 |
|.|.|.|.| |
istore_1 |
..., 3 --> ... |
|.|3|.|.| |
|
int value2 = 4; |
iconst_4 |
... --> ..., 4 |
|.|3|.|.| |
istore_2 |
..., 4 --> ... |
|.|3|4|.| |
|
int result = value1 + value2; |
iload_1 |
... --> ..., 3 |
|.|3|4|.| |
iload_2 |
..., 3 --> ..., 3, 4 |
|.|3|4|.| |
|
iadd |
..., 3, 4 --> ..., 7 |
|.|3|4|.| |
|
istore_3 |
..., 7 --> ... |
|.|3|4|7| |
Wichtige Gruppen von JVM-Befehlen
Die folgende Tabelle zeigt eine Übersicht über wichtige JVM-Befehle (Mnemoniks bzw. Operationscode) und deren Bedeutung. Einige dieser Befehle können zu Gruppen zusammengefasst werden.
Tabelle 4.6. Auswahl einiger Befehle (Mnemoniks und Operationscodes) der Java Virtual Machine und deren Bedeutung.
| Mnemonik | Opcode | Bedeutung |
nop |
0 |
Keine Operation (no operation). |
aconst_null |
1 |
Lege eine null Objekt
reference auf den Operandenstapel.
|
iconst_m1 |
2 |
Lege die int-Konstante -1 auf den
Operandenstapel.
|
iconst_0, ..., iconst_5 |
3, ..., 8 |
Lege int-Konstante (0 bzw. 1,
2, 3, 4, 5) auf den Operandenstapel. Für Werte größer als 5 bzw. kleiner
als 0 wird der Befehl bipush bereitgestellt (z.B.
bipush 9, es werden zwei Bytes für diesen Befehl benötigt).
Der Operand (z.B. die Zahl 3) ist bei diesen Befehlen implizit und es ist
lediglich ein Byte für den entsprechenden Befehl nötig.
|
lconst_0, lconst_1 |
9, 10 |
Lege long-Konstante (0 bzw. 1)
auf den Operandenstapel.
|
fconst_0, ..., fconst_2 |
11, ..., 13 |
Lege float-Konstante (0.0 bzw.
1.0, 2.0) auf den Operandenstapel.
|
dconst_0, dconst_1 |
14, 15 |
Lege double-Konstante (0.0 bzw.
1.0) auf den Operandenstapel.
|
bipush, sipush |
16, 17 |
Lege nachfolgendes Byte bzw. Short auf den
Operandenstack. Dabei wird das Byte bzw. Short (setzt sich aus zwei
nachfolgenden Bytes zusammen) zunächst in einen int-Wert
umgewandelt und dieser wird anschließend auf den Operandenstack gelegt.
|
iload, iload_0, ..., iload_3 |
21, 26, ..., 29 |
Lege einen int-Wert von einer
lokalen Variable auf den Operandenstapel. Bei z.B. iload_3
ist der Index (3) der lokalen Variable im zugehörigen Array (Stichwort:
Frame einer Methode) implizit im Befehl codiert (es wird nur ein Byte
benötigt). Der Bytecode von z.B. iload 9 besteht aus zwei
Bytes und lädt die lokale Variable mit Index 9 auf den Stack.
|
istore, istore_0, ..., istore_3 |
54, 59, ..., 62 |
Speichere den int-Wert, der an
oberster Stelle des Stapels liegt, in das Array der lokalen Variablen.
Der Index dieses Arrays ist bei den 1-Byte Befehlen (z.B. istore_3)
entsprechend angegeben und bei istore wird der Index im
nachfolgenden Byte codiert (z.B. istore 9; der Bytecode dieses
Befehls wäre 36 09; hexadezimal 36 entspricht dezimal 54).
|
pop |
87 |
Nehme oberstes Element vom Operandenstapel. |
dup |
89 |
Verdoppele das oberste Element des Operandenstapels (an der Spitze des Stapels befinden sich nach der Operation zwei gleiche Elemente). |
iadd, ladd, fadd, dadd |
96, ..., 99 |
Nehme die beiden obersten Elemente vom Operandenstack und addiere diese. Lege danach das Ergebnis auf den Stack. Der Buchstabe vor dem add gibt den jeweiligen Typ der Addition bzw. der Operanden an. |
ifeq, ifne, iflt, ifge, ifgt, ifle |
153, ..., 158 |
Verzweige, je nach Vergleich des obersten
Elements (vom Typ int) des Operandenstapels mit dem Wert 0.
|
goto |
167 |
Unbedingte Verzweigung. |
ireturn, lreturn, freturn, dreturn,
areturn, return |
172, ..., 177 |
Gebe einen Rückgabewert an den Methodenaufrufer zurück. |
getstatic, putstatic, getfield, putfield
|
178, ..., 181 |
Setzen bzw. auslesen von Instanzvariablen und Klassenvariablen (statische Variablen). |
invokevirtual, invokespecial, invokestatic,
invokeinterface |
182, ..., 185 |
Aufrufe von Methoden. |
Typkategorien
Bei einigen JVM-Befehlen wie z.B.
pop muss der Typ des
Wertes, der sich an oberster Stelle des Operandenstapels befindet, aus einer
bestimmten Typkategorie stammen. Bei JVM-Befehlen wie z.B.
pop2 wird je nachdem
welchen Typ die Werte des Operandenstapels haben unterschiedlich verfahren. Die
folgende Tabelle zeigt die Zuordnung der tatsächlichen JVM-Typen zu den bei der
Abarbeitung der Befehle (interner Typ) verwendeten Typen:
Tabelle 4.7. Zuordnung: Tatsächlicher Typ - intern verwendeter Typ - Typkategorie.
| Tatsächlicher Typ | Interner Typ | Typkategorie |
boolean |
int |
1 |
byte |
int |
1 |
char |
int |
1 |
short |
int |
1 |
int |
int |
1 |
float |
float |
1 |
reference |
reference |
1 |
returnAddress |
returnAddress |
1 |
long |
long |
2 |
double |
double |
2 |
Es liegen z.B. die Typen boolean und byte bei
der Abarbeitung von Befehlen in einer int-Repräsentation vor (siehe
dazu bastore und
baload).
Ablegen von ganzen Zahlen auf dem Operandenstapel
Unter Verwendung des Datentyps long können ganzzahlige Werte
im Bereich von -263 bis 263-1
gespeichert werden. Wird einer Variablen von einem bestimmten ganzzahligen Datentyp
ein entsprechender Zahlenwert zugewiesen, ist die Übersetzung dieser Anweisung in
Bytecode abhängig vom konkreten Datentyp der Variablen und dem Zahlenwert. Die
Initialisierung einer Variablen mit einem Wert, z.B. mit der auführbaren Anweisung
int a = 2;, wird auf Bytecodeebene dadurch realisiert, dass zunächst
der Zahlenwert 2 auf einen entsprechenden Operandenstapel gelegt wird, wobei je
nach Größe der Zahl unterschiedliche JVM-Befehle für diese Operation verwendet
werden. Die folgende Übersicht zeigt verschiedene Zahlenbereiche und die JVM-Befehle,
die bei der Compilierung erzeugt werden:
| Zahlenbereich | Verwendeter JVM-Befehl | Typ der Variablen |
| -263 ... -231-1 | ldc2_w |
long |
| -231 ... -32769 | ldc,
ldc_w |
int |
| -32768 ... -129 | sipush |
short, int |
| -128 ... -2 | bipush |
byte, short, int |
| -1 | iconst_m1
|
byte, short, int |
| 0 | iconst_0
|
byte, short, int |
| 1 | iconst_1
|
byte, short, int |
| 2 | iconst_2
|
byte, short, int |
| 3 | iconst_3
|
byte, short, int |
| 4 | iconst_4
|
byte, short, int |
| 5 | iconst_5
|
byte, short, int |
| 6 ... 127 | bipush
|
byte, short, int |
| 128 ... 32767 | sipush
|
short, int |
| 32768 ... 231-1 | ldc,
ldc_w |
int |
| 231 ... 263-1 | ldc2_w
|
long |
Es kann z.B. für die Zuweisung des Zahlenwertes 2 an eine Variable sowohl
der JVM-Befehl iconst_2 als auch ldc2_w durch den
Übersetzer erzeugt werden, abhängig vom Typ der Variablen (z.B. byte
oder int bzw. long). Mit lconst_0 und
lconst_1 werden zwei Ein-Byte-Befehle für das Ablegen der
Long-Konstanten 0 bzw. 1 auf den Operandenstapel zur Verfügung gestellt, analog
zu den entsprechenden Integer-Befehlen iconst_0 und iconst_1.
Die folgenden kurzen Beispiele zeigen die Übersetzungen durch den Java-Compiler
bei unterschiedlichen Datentypen:
byte a = 2; 0: iconst_2
1: istore_1
int a = 2; 0: iconst_2
1: istore_1
long a = 2; 0: ldc2_w #2; //long 2L
3: lstore_1
long a = 1; 0: lconst_1
1: lstore_1Für das Ablegen von Gleitkommazahlen enthält der JVM-Befehlssatz die
einzelnen Ein-Byte-Befehle fconst_x und dconst_x
(x ist Platzhalter für einfache Konstanten wie z.B. 1.0). Alle anderen
Gleitkommazahlen werden ebenfalls mit ldc bzw. ldc_w
und ldc2_w auf den Stapel gelegt, indem auf eine entsprechende
Konstante im Konstantenpool verwiesen wird.
Binärdarstellung einer Gleitkommazahl (32 Bit)
Die Binärdarstellung der Gleitkommazahl 3.0 durch 32 Bit ist wie folgt aufgebaut:
Bit 31: 0 Vorzeichen (1 Bit) Bits 30-23: 10000000 Exponent (8 Bits) Bits 22-0: 1000000 00000000 00000000 Mantisse (23 Bits)
Ist das 31. Bit (Vorzeichenbit) in der Binärdarstellung 0, dann handelt es sich um eine positive Zahl. Bei einer negativen Gleitkommazahl ist das höchstwertige Bit 1. Mit der folgenden Gleichung können die Bits 30-23 der Binärdarstellung einer Gleitkommazahl ermittelt werden:
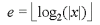
Zunächst wäre für x die im Beispiel verwendete Zahl 3.0 zu setzen. Der
Logarithmus von 3.0 zur Basis 2 lautet dann 1.5850 (gerundet). Die beiden Zeichen,
die den Logarithmusausdruck einschließen, entsprechen Math.floor;
für Math.floor(1.5850) ist das Ergebnis die ganze Zahl 1 und damit
e = 1. Der Zahlenwert e wird jedoch nicht direkt durch die 8 Exponentenbits codiert,
sondern es wird zu diesem Wert noch ein sogenannter Biaswert
addiert, den die Norm IEEE 754 mit B = 127 festlegt (single bzw. 32 Bit). Durch
die Verwendung eines Biaswertes (dt. Verzerrungswert) können die 8 Exponentenbits
ohne Vorzeichen gewertet werden und der darstellbare Dezimalzahlenbereich geht von
0 bis 255. Es ergibt sich im Beispiel:
e = 1 E = e + B = 1 + 127 = 128 = (10000000)b
Nachdem die Bits 30-23 mit 10000000 ermittelt wurden, soll nun
der unterste Bitblock (Mantisse) mit Hilfe der folgenden Gleichung errechnet
werden:
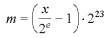
Wird x durch den Beispielwert 3.0 und e durch den zuvor errechneten Wert 1 ersetzt, führt dies über das Zwischenergebnis (1.5 - 1) * 223 zu:
m = 4194304 = (1000000 00000000 00000000)b
Werden nun die drei ermittelten Bitblöcke zusammengesetz, ergibt sich die binäre Darstellung (einfache Genauigkeit bzw. 32 Bit) der Gleitkommazahl 3.0:
0 10000000 10000000000000000000000
Die binäre Darstellung der Zahl 3.0 kann mit Hilfe der folgenden Anweisungen gewonnen werden:
int a = Float.floatToIntBits(3.0f); String s = Integer.toBinaryString(a); System.out.println(s);
Führende Nullen werden bei der Ausgabe nicht beachtet, d.h. Bit 31 wird nicht mit ausgegeben, da es den Wert 0 besitzt.
Umrechnung: 32 Bits einer Gleitkommazahl - Dezimalzahlenwert
Die Binärdarstellung der Gleitkommazahl -3.7 durch 32 Bit ist wie folgt aufgebaut:
Bit 31: 1 Vorzeichen (1 Bit) Bits 30-23: 10000000 Exponent (8 Bits) Bits 22-0: 1101100 11001100 11001101 Mantisse (23 Bits)
Das Vorzeichen der negativen Zahl -3.7 wird in der Binärdarstellung durch Setzen von Bit 31 berücksichtigt. Mit der folgenden Gleichung kann eine gegebene Bitfolge, die eine Gleitkommazahl repräsentiert, in einen Dezimalzahlenwert z umgerechnet werden:
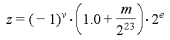
Der Wert v, der das Vorzeichen der Gleitkommazahl bestimmt, wird durch Bit
31 festgelegt. Zur Ermittlung von e tragen die 8 Exponentenbits 10000000
und ein sogenannter Biaswert (dt. Verzerrungswert) bei, der
durch IEEE 754 mit B = 127 festgelegt ist (single bzw. 32 Bit). Der Zahlenwert
für m wird binär durch die Bits 22-0 repräsentiert. Die drei Größen zur Berechnung
von z ergeben sich wie folgt:
v = (1)b = 1 e = E - B = (10000000)b - 127 = 128 - 127 = 1 m = (1101100 11001100 11001101)b = 7130317
Werden die ermittelten Zahlen in die entsprechende Gleichung eingesetzt, ergibt sich über das Zwischenergebnis z = (-1)1 * (1.0 + 7130317 / 8388608) * 2 das auf vier Nachkommastellen gerundete Endergebnis zu:
z = -3.7000
Umrechnung der Wertemengen von Gleitkommazahlen (Value Set Conversion)
Bei der Abarbeitung von float- und double-Typen
wird unter bestimmten Bedingungen eine Value Set Conversion
(dt. Umrechnung der Wertemenge) vorgenommen, falls eine Umrechnung zwischen
verschiedenen Wertebereichen der Gleitkommazahlen möglich bzw. notwendig ist.
Grundlage einer "Value Set Conversion" ist die Norm IEEE 754, die
Standarddarstellungen für binäre Gleitkommazahlen definiert und u.a. Verfahren
für die Durchführung mathematischer Operationen festlegt. IEEE 754 definiert die
beiden Grundformate für binäre Gleitkommazahlen 32 Bit (single precision) und 64
Bit (double precision) und zwei erweiterte Formate.
Diese Umwandlung vom Gleitkommawerten ist abhängig von der Implementierung der
virtuellen Java-Maschine. Eine JVM, die einen erweiterten Wertebereich für
Gleitkommazahlen unterstützt, kann bzw. muss eine Gleitkommazahl einem erweiterten
Wertebereich bzw. einem Standardwertebereich zuordnen können.
Bei dieser Umrechnung von Wertemengen wird der Typ float bzw.
double nicht geändert. Eine Umrechnung wird vorgenommen wenn ein Wert
vom Typ float bzw. double kein Element eines festgelegten
float- bzw. double-Wertebereiches ist. Der ursprüngliche
Wert wird dann dem am nächsten liegenden Wert innerhalb des geforderten
Wertebereiches zugeordnet.
Tabelle 4.8. Operationscodes und zugehörige Mnemoniks der Java Virtual Machine.
| Opcode | Mnemonik | |
0 |
0x00 |
nop |
1 |
0x01 |
aconst_null |
2 |
0x02 |
iconst_m1 |
3 |
0x03 |
iconst_0 |
4 |
0x04 |
iconst_1 |
5 |
0x05 |
iconst_2 |
6 |
0x06 |
iconst_3 |
7 |
0x07 |
iconst_4 |
8 |
0x08 |
iconst_5 |
9 |
0x09 |
lconst_0 |
10 |
0x0a |
lconst_1 |
11 |
0x0b |
fconst_0 |
12 |
0x0c |
fconst_1 |
13 |
0x0d |
fconst_2 |
14 |
0x0e |
dconst_0 |
15 |
0x0f |
dconst_1 |
16 |
0x10 |
bipush |
17 |
0x11 |
sipush |
18 |
0x12 |
ldc |
19 |
0x13 |
ldc_w |
20 |
0x14 |
ldc2_w |
21 |
0x15 |
iload |
22 |
0x16 |
lload |
23 |
0x17 |
fload |
24 |
0x18 |
dload |
25 |
0x19 |
aload |
26 |
0x1a |
iload_0 |
27 |
0x1b |
iload_1 |
28 |
0x1c |
iload_2 |
29 |
0x1d |
iload_3 |
30 |
0x1e |
lload_0 |
31 |
0x1f |
lload_1 |
32 |
0x20 |
lload_2 |
33 |
0x21 |
lload_3 |
34 |
0x22 |
fload_0 |
35 |
0x23 |
fload_1 |
36 |
0x24 |
fload_2 |
37 |
0x25 |
fload_3 |
38 |
0x26 |
dload_0 |
39 |
0x27 |
dload_1 |
40 |
0x28 |
dload_2 |
41 |
0x29 |
dload_3 |
42 |
0x2a |
aload_0 |
43 |
0x2b |
aload_1 |
44 |
0x2c |
aload_2 |
45 |
0x2d |
aload_3 |
46 |
0x2e |
iaload |
47 |
0x2f |
laload |
48 |
0x30 |
faload |
49 |
0x31 |
daload |
50 |
0x32 |
aaload |
51 |
0x33 |
baload |
52 |
0x34 |
caload |
53 |
0x35 |
saload |
54 |
0x36 |
istore |
55 |
0x37 |
lstore |
56 |
0x38 |
fstore |
57 |
0x39 |
dstore |
58 |
0x3a |
astore |
59 |
0x3b |
istore_0 |
60 |
0x3c |
istore_1 |
61 |
0x3d |
istore_2 |
62 |
0x3e |
istore_3 |
63 |
0x3f |
lstore_0 |
64 |
0x40 |
lstore_1 |
65 |
0x41 |
lstore_2 |
66 |
0x42 |
lstore_3 |
67 |
0x43 |
fstore_0 |
68 |
0x44 |
fstore_1 |
69 |
0x45 |
fstore_2 |
70 |
0x46 |
fstore_3 |
71 |
0x47 |
dstore_0 |
72 |
0x48 |
dstore_1 |
73 |
0x49 |
dstore_2 |
74 |
0x4a |
dstore_3 |
75 |
0x4b |
astore_0 |
76 |
0x4c |
astore_1 |
77 |
0x4d |
astore_2 |
78 |
0x4e |
astore_3 |
79 |
0x4f |
iastore |
80 |
0x50 |
lastore |
81 |
0x51 |
fastore |
82 |
0x52 |
dastore |
83 |
0x53 |
aastore |
84 |
0x54 |
bastore |
85 |
0x55 |
castore |
86 |
0x56 |
sastore |
87 |
0x57 |
pop |
88 |
0x58 |
pop2 |
89 |
0x59 |
dup |
90 |
0x5a |
dup_x1 |
91 |
0x5b |
dup_x2 |
92 |
0x5c |
dup2 |
93 |
0x5d |
dup2_x1 |
94 |
0x5e |
dup2_x2 |
95 |
0x5f |
swap |
96 |
0x60 |
iadd |
97 |
0x61 |
ladd |
98 |
0x62 |
fadd |
99 |
0x63 |
dadd |
100 |
0x64 |
isub |
101 |
0x65 |
lsub |
102 |
0x66 |
fsub |
103 |
0x67 |
dsub |
104 |
0x68 |
imul |
105 |
0x69 |
lmul |
106 |
0x6a |
fmul |
107 |
0x6b |
dmul |
108 |
0x6c |
idiv |
109 |
0x6d |
ldiv |
110 |
0x6e |
fdiv |
111 |
0x6f |
ddiv |
112 |
0x70 |
irem |
113 |
0x71 |
lrem |
114 |
0x72 |
frem |
115 |
0x73 |
drem |
116 |
0x74 |
ineg |
117 |
0x75 |
lneg |
118 |
0x76 |
fneg |
119 |
0x77 |
dneg |
120 |
0x78 |
ishl |
121 |
0x79 |
lshl |
122 |
0x7a |
ishr |
123 |
0x7b |
lshr |
124 |
0x7c |
iushr |
125 |
0x7d |
lushr |
126 |
0x7e |
iand |
127 |
0x7f |
land |
128 |
0x80 |
ior |
129 |
0x81 |
lor |
130 |
0x82 |
ixor |
131 |
0x83 |
lxor |
132 |
0x84 |
iinc |
133 |
0x85 |
i2l |
134 |
0x86 |
i2f |
135 |
0x87 |
i2d |
136 |
0x88 |
l2i |
137 |
0x89 |
l2f |
138 |
0x8a |
l2d |
139 |
0x8b |
f2i |
140 |
0x8c |
f2l |
141 |
0x8d |
f2d |
142 |
0x8e |
d2i |
143 |
0x8f |
d2l |
144 |
0x90 |
d2f |
145 |
0x91 |
i2b |
146 |
0x92 |
i2c |
147 |
0x93 |
i2s |
148 |
0x94 |
lcmp |
149 |
0x95 |
fcmpl |
150 |
0x96 |
fcmpg |
151 |
0x97 |
dcmpl |
152 |
0x98 |
dcmpg |
153 |
0x99 |
ifeq |
154 |
0x9a |
ifne |
155 |
0x9b |
iflt |
156 |
0x9c |
ifge |
157 |
0x9d |
ifgt |
158 |
0x9e |
ifle |
159 |
0x9f |
if_icmpeq |
160 |
0xa0 |
if_icmpne |
161 |
0xa1 |
if_icmplt |
162 |
0xa2 |
if_icmpge |
163 |
0xa3 |
if_icmpgt |
164 |
0xa4 |
if_icmple |
165 |
0xa5 |
if_acmpeq |
166 |
0xa6 |
if_acmpne |
167 |
0xa7 |
goto |
168 |
0xa8 |
jsr |
169 |
0xa9 |
ret |
170 |
0xaa |
tableswitch |
171 |
0xab |
lookupswitch |
172 |
0xac |
ireturn |
173 |
0xad |
lreturn |
174 |
0xae |
freturn |
175 |
0xaf |
dreturn |
176 |
0xb0 |
areturn |
177 |
0xb1 |
return |
178 |
0xb2 |
getstatic |
179 |
0xb3 |
putstatic |
180 |
0xb4 |
getfield |
181 |
0xb5 |
putfield |
182 |
0xb6 |
invokevirtual |
183 |
0xb7 |
invokespecial |
184 |
0xb8 |
invokestatic |
185 |
0xb9 |
invokeinterface |
186 |
0xba |
xxxunusedxxx |
187 |
0xbb |
new |
188 |
0xbc |
newarray |
189 |
0xbd |
anewarray |
190 |
0xbe |
arraylength |
191 |
0xbf |
athrow |
192 |
0xc0 |
checkcast |
193 |
0xc1 |
instanceof |
194 |
0xc2 |
monitorenter |
195 |
0xc3 |
monitorexit |
196 |
0xc4 |
wide |
197 |
0xc5 |
multianewarray |
198 |
0xc6 |
ifnull |
199 |
0xc7 |
ifnonnull |
200 |
0xc8 |
goto_w |
201 |
0xc9 |
jsr_w |
202 |
0xca |
breakpoint |
203 |
||
204 |
||
205 |
||
206 |
||
207 |
||
208 |
||
209 |
||
210 |
||
211 |
||
212 |
||
213 |
||
214 |
||
215 |
||
216 |
||
217 |
||
218 |
||
219 |
||
220 |
||
221 |
||
222 |
||
223 |
||
224 |
||
225 |
||
226 |
||
227 |
||
228 |
||
229 |
||
230 |
||
231 |
||
232 |
||
233 |
||
234 |
||
235 |
||
236 |
||
237 |
||
238 |
||
239 |
||
240 |
||
241 |
||
242 |
||
243 |
||
244 |
||
245 |
||
246 |
||
247 |
||
248 |
||
249 |
||
250 |
||
251 |
||
252 |
||
253 |
||
254 |
0xfe |
impdep1 |
255 |
0xff |
impdep2 |